Il calcolo "geometrico" di $\pi$¶
Archimede 225 A. C.¶
Area delle superfici dei poligoni regolari di $2^n$ lati inscritti in un cerchio di raggio unitario.
$p_n = \dfrac{2^n \overline{OA}\overline{BH}}{2} = 2^{n-1}\sin \beta$ dove $\beta = \dfrac{2 \pi}{2^n}$
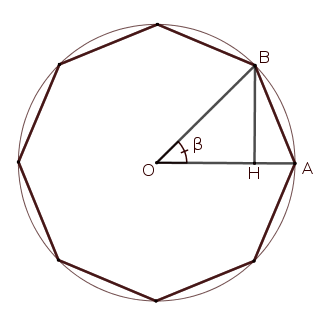
$\sin \beta = \sqrt{\dfrac{1 -\cos(2 \beta)}{2}}=\sqrt{\dfrac{1-\sqrt{1-\sin^2(2 \beta)}}{2}}$, $0 \leq \beta \leq \dfrac{\pi}{4}$
import math
import matplotlib.pyplot as plt
import numpy as np
from tabulate import tabulate
# primo passo il quadrato
archimede = []
seno = math.sqrt(2)/2
b = 4
n = 28
for i in range(1,n):
p = b*seno
archimede.append(p)
seno = math.sqrt((1-math.sqrt(1-seno**2))/2)
b = 2*b
archimede = np.array(archimede, dtype=np.float64)
Viete 1593¶
Metà del perimetro dei poligoni di $2^n$ lati inscritti in una circonferenza di raggio unitario.
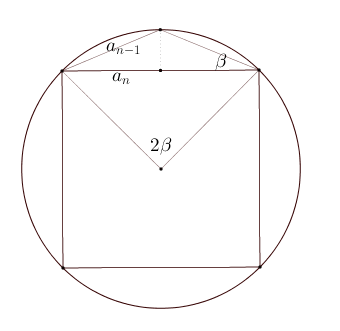$p_n = 2^{n-1}a_n$ dove $a_{n+1}=\cos \left( \dfrac{\pi}{2^{n+1}} \right) = \dfrac{a_n}{2}$
$p_{n+1}=2^n a_{n+1}$ e utilizzando $\cos \beta = \sqrt{\dfrac{1+\cos(2 \beta)}{2}}$ si ha:
viete = []
coseno = 0
p = 2
for i in range(1,n):
coseno = math.sqrt((1+coseno)/2)
p = p/coseno
viete.append(p)
viete = np.array(viete, dtype=np.float64)
Poligoni regolari circoscritti¶
Metà del perimetro del poligono regolare di $2^n$ lati circosritto alla circonferenza unitaria.
$p_n = 2^n \overline{HB} \overline{OH} = 2^n \overline{HB}$ dove $\overline{HB}= \overline{OH} tg(\beta)$
$tg(\beta) = \dfrac{\sqrt{1-tg^2(2 \beta)}-1}{tg(2 \beta)}$
tgb = 1
polext = []
for h in range(1,n):
p = 2**(h+1)*tgb
polext.append(p)
tgb = (math.sqrt(1+tgb**2)-1)/tgb
polext = np.array(polext, dtype=np.float64)
Sintesi¶
# numerica
rip = np.arange(2,n+1,1)
print(tabulate({"n": rip,"Archimede": archimede,"Viete": viete,"Poligoni circoscritti": polext}, headers="keys"))
# grafica
figura = plt.figure(figsize=(10, 10),dpi=100)
plt.ylim(ymax = 3.3, ymin = 3.0)
plt.plot(rip,archimede,'b-')
plt.plot(rip,viete,'k-')
plt.plot(rip,polext,'r-')
plt.show()
